Question 117433: Multiply
(m-4n)(m-4n)
Found 2 solutions by jim_thompson5910, bucky:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given to multiply:
.
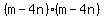
.
One way to do this is to multiply using the FOIL rule ... multiply the First terms in each set
of parentheses (in this case m times m), then multiply the Outside terms (m times - 4n), then
multiply the Inside terms (-4n times m), and then multiply the Last terms (-4n times -4n).
Then you simplify the results by combining like terms.
.
I prefer to look at it in a little different fashion because the FOIL rule (firsts, outsides
insides, lasts) is really set up for binomials ... two sets of parentheses with two terms in
each set. The approach I use works just as well, but it works no matter how many terms are in
each set of parentheses.
.
The approach I use is to take the first term in the first set of parentheses and use it to
multiply each of the terms in the second set of parentheses. Once that is done, take the second
term in the first set of parentheses and use it to multiply each of the terms in the second set
of parentheses. If there are more terms in the first set of parentheses, just take them one
at a time and use them to multiply all the terms in the second set of parentheses. Once
that is done, simplify the results by combining like terms in all the products.
.
In this problem you had:
.
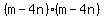
.
Take the m in the first set of parentheses and multiply it by the m and then by the -4n in
the second set of parentheses and you get a product of:
.
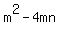
.
Next take the second term in the first set of parentheses ... -4n and use it to multiply each of
the terms in the second set of parentheses. When you do, you get a product of:
.
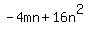
.
Now combine all the terms. The two products are:
.
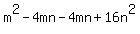
.
Note that the terms -4mn and -4mn combine to give -8mn. There are no other common terms.
So, as the answer you have:
.
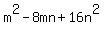
.
Hope this helps you to understand a way of multiplying two quantities, each with multiple terms.
.
|
|
|