Tutors Answer Your Questions about Sequences-and-series (FREE)
Question 265521: The sum of two numbers is less than or equal to 23 . The second number is 7 less than the first. What are the possible values for the first of the two numbers? I cannot come up with an answer for this one and I am getting frustrated can someone please help me, thank you.
Click here to see answer by roseo(33)  |
Question 266760: If someone could please help me with this problem, it would be greatly appreciated!
I have to find the sum of the geometric sequence
 , , 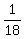 , ... , ... 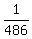
This is what I have so far:
r=(1/3)

(it's supposed to be (n-1))
from this I got n=5
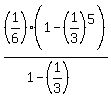

As elementary as this is, I need help finding the sum and understanding the process(es) of how to work this equation when fractions are in the mix. (That is, unless I've made mistakes prior to getting to this point.)
Click here to see answer by Edwin McCravy(20056)   |
Question 266760: If someone could please help me with this problem, it would be greatly appreciated!
I have to find the sum of the geometric sequence
 , , 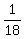 , ... , ... 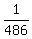
This is what I have so far:
r=(1/3)

(it's supposed to be (n-1))
from this I got n=5
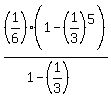

As elementary as this is, I need help finding the sum and understanding the process(es) of how to work this equation when fractions are in the mix. (That is, unless I've made mistakes prior to getting to this point.)
Click here to see answer by stanbon(75887)  |
Question 270153: 3, 5,–5...
The first term in the sequence of numbers shown above is 3. Each even–numbered term is 2 more than the previous term and each odd–numbered term, after the first, is –1 times the previous term. For example, the second term is 3 + 2, and the third term is (–1) × 5. What is the 55th term of the sequence?
(A)–5 (B) –3 (C) –1 (D) 3 (E) 5
Click here to see answer by Edwin McCravy(20056)   |
Question 271227: Ineed some helpw with the following two questions...
1. Compute the sum of the following unsigned integers. 0b11000100 + 0b00110110
2. How many bits are required to represent the decimal number 1497 as unsigned binary integer?
Click here to see answer by Stitch(470)  |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790
|







