Question 1210233: Show that the sum of n terms of the progression
log(x), log(x^2), log(x^3), log(x^4) , ..., log(x^n) is (n*(n+1)/2)*log x.
Found 3 solutions by Edwin McCravy, ikleyn, mccravyedwin:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I did not understand the problem, so I deleted what I thought it meant.
Ikleyn's solution is correct. Notice that I changed the wording of the original
problem to her edited wording. I think we tutors should change the wording of the
original problem whenever it is not easily understandable as written.
Edwin
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show that the sum of the end term of the progression Log x, Log x^2, Log x^3, log x^4 = n (n+1/2) Log x
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Wording and writing in the post are incorrect, so I edited it to make sense from nonsense.
My edited formulation is as follows:
Show that the sum of n terms of the progression log(x), log(x^2), log(x^3), log(x^4) , . . , log(x^n) is (n*(n+1)/2)*log x.
Below is my solution for this edited formulation.
In this problem, x > 0.
Let a = log(x).
Then 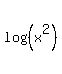 = 2a, = 2a, 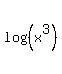 = 3a, . . . and so on . . . till = 3a, . . . and so on . . . till 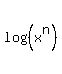 = n*a.
Therefore, our progression takes the form
a + 2a + 3a + . . . + n*a = (1 + 2 + 3 + . . . + n)*a.
The sum in parentheses in the right side is well known sum of the arithmetic progression,
and it is equal to = n*a.
Therefore, our progression takes the form
a + 2a + 3a + . . . + n*a = (1 + 2 + 3 + . . . + n)*a.
The sum in parentheses in the right side is well known sum of the arithmetic progression,
and it is equal to  .
Thus .
Thus 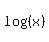 + + 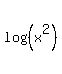 + + 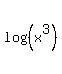 + . . . + + . . . + 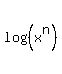 = =  .
It is the final answer, and the proof is complete. .
It is the final answer, and the proof is complete.
Solved.
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn's solution is correct as she interpreted it. Sometimes English is not
the first language of the student, and the way they translate things into English
is not always the same way we express things in the US.
Edwin
|
|
|