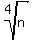SOLUTION: For a positive integer n, let f(n) denote the integer that is closest to {{{root(4,n)}}}. Find the integer m so that {{{sum(f(n),n=1,m)}}}{{{""=""}}}{{{100}}}.

First column of the table in the counter of natural numbers n = 1, 2, 3, . . . 

Second column is the values of 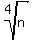, rounded to the closest integer number.

Third column is the sum S(n) of the first n integer numbers of the second column.


The table shows that the integer 'm' such that the sum S(m) is precisely 
equal to 100  is 48.


n 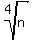                        S(n)
-----------------------------------------------    

1		1		1
2		1		2
3		1		3
4		1		4
5		1		5
6		2		7
7		2		9
8		2		11
9		2		13
10		2		15
11		2		17
12		2		19
13		2		21
14		2		23
15		2		25
16		2		27
17		2		29
18		2		31
19		2		33
20		2		35
21		2		37
22		2		39
23		2		41
24		2		43
25		2		45
26		2		47
27		2		49
28		2		51
29		2		53
30		2		55
31		2		57
32		2		59
33		2		61
34		2		63
35		2		65
36		2		67
37		2		69
38		2		71
39		2		73
40		3		76
41		3		79
42		3		82
43		3		85
44		3		88
45		3		91
46		3		94
47		3		97
48		3		100    <<<---===


So, the ANSWER to the problem's question is  m = 48.


Having this table, one can construct a wording solution, retelling this my solution in wording form
without using this table, but I prefer direct arguments.

For a positive integer n, let f(n) denote the integer that is closest to
.  Find the integer m so that
.




So terms 1 through 5 are all 1's.  That's 5-1+1 = 5 terms of 1's
We have 5 terms so far. And so far the sum is 5x1 = 5.




So terms 6 through 39 are all 2's.  That's 39-6+1=34 terms of 2's.
We have 5+34=39 terms so far. And so far the sum is 5 + 34x2 = 5 + 68 = 73




So terms from 39 on are all 3's.  So we only need to know how many more terms of
3's we need beyond the 39 terms to raise the sum of 73 to 100.

We need to raise the sum by 100-73=27 which will require 27/3=9 more terms of 3's.

So the total number of terms will be 39+9 = 48.

So m = 48

Edwin