Question 1209818: .
Found 3 solutions by CPhill, ikleyn, greenestamps:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's find the first few terms of the sequence:
* $a_0 = 1$
* $a_2 = 2$
* $a_{n+2} = \frac{a_{n+1}}{a_n}$
We need to find $a_1$. We can use the formula with $n=0$:
$a_2 = \frac{a_1}{a_0}$
$2 = \frac{a_1}{1}$
$a_1 = 2$
Now, let's find more terms:
* $a_3 = \frac{a_2}{a_1} = \frac{2}{2} = 1$
* $a_4 = \frac{a_3}{a_2} = \frac{1}{2}$
* $a_5 = \frac{a_4}{a_3} = \frac{1/2}{1} = \frac{1}{2}$
* $a_6 = \frac{a_5}{a_4} = \frac{1/2}{1/2} = 1$
* $a_7 = \frac{a_6}{a_5} = \frac{1}{1/2} = 2$
* $a_8 = \frac{a_7}{a_6} = \frac{2}{1} = 2$
* $a_9 = \frac{a_8}{a_7} = \frac{2}{2} = 1$
* $a_{10} = \frac{a_9}{a_8} = \frac{1}{2}$
* $a_{11} = \frac{a_{10}}{a_9} = \frac{1/2}{1} = \frac{1}{2}$
* $a_{12} = \frac{a_{11}}{a_{10}} = \frac{1/2}{1/2} = 1$
The sequence is periodic with period 6: 1, 2, 2, 1, 1/2, 1/2, 1, 2, 2, 1, 1/2, 1/2, ...
The sum of the terms in one period is:
$1 + 2 + 2 + 1 + \frac{1}{2} + \frac{1}{2} = 7$
We want to find $a_0 + a_1 + a_2 + \dots + a_{100}$.
Since the period is 6, we can divide 101 by 6:
$101 = 16 \cdot 6 + 5$
So there are 16 full periods and 5 remaining terms.
The sum of the 16 full periods is $16 \cdot 7 = 112$.
The remaining 5 terms are $a_{96}, a_{97}, a_{98}, a_{99}, a_{100}$, which are the same as $a_0, a_1, a_2, a_3, a_4$:
$1, 2, 2, 1, \frac{1}{2}$
The sum of these 5 terms is $1 + 2 + 2 + 1 + \frac{1}{2} = \frac{13}{2} = 6.5$.
Therefore, the sum of the first 101 terms is:
$112 + \frac{13}{2} = \frac{224}{2} + \frac{13}{2} = \frac{237}{2} = 118.5$
Final Answer: The final answer is $\boxed{118.5}$
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A sequence of real numbers (a_n) is defined as follows: a_0 = 1, a_2 = 2, and
a_{n + 2} = \frac{a_{n + 1}}{a_n}
for n = 0, 1, 2, \dots. Find a_0 + a_1 + a_2 + \dots + a_{100}.
~~~~~~~~~~~~~~~~~~~~~~~~~
The problem's formulation in your post is INCORRECT
The correct formulation is as follows:
A sequence of real numbers (a_n) is defined as follows: a_0 = 1,  a_1 = 2, and a_1 = 2, and
a_{n + 2} = \frac{a_{n + 1}}{a_n}
for n = 0, 1, 2, \dots. Find a_0 + a_1 + a_2 + \dots + a_{100}.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The AI solution from the other "tutor" has the right final answer, but the AI presentation is hard to follow. Here is a solution in English....



Although the given starting information is not standard, we can use the recursive definition with the given values of 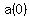 and and 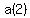 to find to find 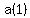 and then use the recursive definition to find all subsequent terms. and then use the recursive definition to find all subsequent terms.
For n=0....



So the first three terms are 1, 2, and 2.
Note that the first term is 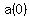 and the problem asks for the sum of the terms through and the problem asks for the sum of the terms through 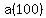 , so we are looking for the sum of the first 101 terms. , so we are looking for the sum of the first 101 terms.






We now see that the terms of the sequence follow a cyclic pattern of length 6:
1, 2, 2, 1, 1/2, 1/2
With a cycle of length 6, 101 terms will mean 16 times through the cycle plus 5 more terms.
The sum of the numbers in each cycle is 7; the sum of the numbers in 16 cycles is 16*7 = 112.
The sum of the first 5 numbers in each cycle is 6.5.
The sum of the first 101 terms is 112+6.5 = 118.5
ANSWER: 118.5
|
|
|