Question 1209805: Let a_1 + a_2 + a_3 + dotsb be an infinite geometric series with positive terms. If a_2 = 10, then find the smallest possible value of
a_1 + a_2 + a_3.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
Understanding Geometric Series
A geometric series has the form: a, ar, ar², ar³, ...
a is the first term (a_1)
r is the common ratio
a_n = ar^(n-1)
Given Information
The series has positive terms, so a > 0 and r > 0.
a_2 = 10
Finding a_1 and r
a_2 = ar^(2-1) = ar
ar = 10
a = 10/r
Finding a_1 + a_2 + a_3
a_1 + a_2 + a_3 = a + ar + ar²
Substitute a = 10/r:
(10/r) + 10 + 10r
Minimizing a_1 + a_2 + a_3
Let S = (10/r) + 10 + 10r. We want to minimize S.
Take the derivative with respect to r:
dS/dr = -10/r² + 10
Set the derivative to zero and solve for r:
-10/r² + 10 = 0
10 = 10/r²
r² = 1
r = ±1
Consider positive r:
Since the terms are positive, r must be positive. Therefore, r = 1.
Check the second derivative:
d²S/dr² = 20/r³
When r = 1, d²S/dr² = 20 > 0, which means we have a minimum.
Find a_1:
a = 10/r = 10/1 = 10
Find a_1 + a_2 + a_3:
a_1 + a_2 + a_3 = 10 + 10 + 10 = 30
However, we need to consider the behavior of the function as r approaches 0 or infinity.
As r approaches 0, 10/r approaches infinity, so S approaches infinity.
As r approaches infinity, 10r approaches infinity, so S approaches infinity.
Therefore, the minimum value of a_1 + a_2 + a_3 occurs when r = 1, and the minimum value is 30.
Final Answer: The smallest possible value of a_1 + a_2 + a_3 is 30.
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let a_1 + a_2 + a_3 + dots be an infinite geometric series with positive terms.
If a_2 = 10, then find the smallest possible value of a_1 + a_2 + a_3.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is simple and elementary, and I will show below
a simple solution without using Calculus and/or derivatives.
The fact that this geometric progression has positive terms tells us
that the first term  is positive and the common ratio is positive, too.
So, the sum is positive and the common ratio is positive, too.
So, the sum 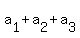 can be presented in the form can be presented in the form
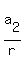 + +  + + 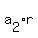 = = 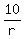 + 10 + 10*r. (1)
We can identically transform this expression in the right side of (1) this way + 10 + 10*r. (1)
We can identically transform this expression in the right side of (1) this way
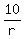 + 10 + 10r = ( + 10 + 10r = (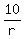 - 20 + 10r) + 30 = - 20 + 10r) + 30 = 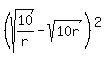 + 30. (2)
Now, the part + 30. (2)
Now, the part 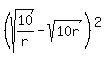 is always greater than or equal to zero,
since it is the square of real number.
Hence, this expression is minimal if and only if is always greater than or equal to zero,
since it is the square of real number.
Hence, this expression is minimal if and only if
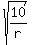 = = 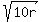 , (3)
when , (3)
when 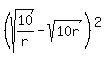 is equal to zero.
Square both sides in (3) is equal to zero.
Square both sides in (3)
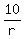 = 10r,
or = 10r,
or
 = r, --> 1 = r^2 --> r = = r, --> 1 = r^2 --> r = 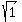 = 1.
Hence, the sum (1) is minimal if and only if r = 1.
Then the sum (1) is = 1.
Hence, the sum (1) is minimal if and only if r = 1.
Then the sum (1) is 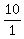 + 10 + 10*1 = 10 + 10 + 10 = 30.
At this point, the solution is complete.
ANSWER. The sum + 10 + 10*1 = 10 + 10 + 10 = 30.
At this point, the solution is complete.
ANSWER. The sum 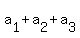 of geometric progression with positive terms
is minimal if and only if the common ratio r is 1.
It is the case when all three terms of the progression are equal.
For our case, this minimal value of the sum of the first three terms is 30, i.e. thrice its central term. of geometric progression with positive terms
is minimal if and only if the common ratio r is 1.
It is the case when all three terms of the progression are equal.
For our case, this minimal value of the sum of the first three terms is 30, i.e. thrice its central term.
Solved completely.
----------------------------
As this problem is worded and presented, it considers only three first terms of the geometric progression.
Therefore, in the problem's formulation, there is no any need to consider an infinite progression.
Good style tells us to consider only three-term geometric progression from the very beginning.
Moreover, an infinite geometric progression with r= 1 diverges and its sum does not exist (is infinity).
|
|
|