Question 998498: three numbers are in arithmetic progression. their sum and sum of their squares is 126. find the smallest number of the arithmetic progression
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be a middle term of this arithmetic progression.
Then two other terms are x-d and x+d, where d is the common difference.
The sum of three members is (x-d) + x + (x+d) = 3x.
It is 126, hence, x = 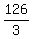 = 42. = 42.
Now, we need to find d. For it, we have another equation
 = =  , or , or
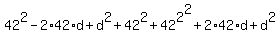 = =  , or , or
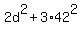 = =  , ,
 = = 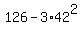 . .
Hey, the right side is negative! While the left side is always non-negative.
Your problem has no solution.
Truly, I spent my time for nothing, working on this problem.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! three numbers are in arithmetic progression. their sum is 18
and the sum of their squares is 126. find the smallest number
of the arithmetic progression.
[The lady above showed that your problem has no solution as
you stated it. That's because you did not give the sum of
the numbers and it appeared that the sum of the numbers was
also 126. But since that gives no solution, I arbitrarily
assumed it was 18 since that or -18 were the only numbers
that would give a reasonable answer. But please be careful
next time to copy the problem exactly.]
Let the three numbers be a-d, a, and a+d.
Those are in arithmetic progression because:
1. If we add d to the first term, which is a-d, we get
(a-d)+d or a, which is the second term.
2. If we add d to the second term, which is a, we get
a+d which is the third term.
Their sum is 18 and the sum of their squares is 126.
1) (a-d)+a+(a+d) = 18
2) (a-d)²+a²+(a+d)² = 126
Simplifying equation 1):
3a = 18
a = 6
Substituting a = 6 in the equation 2):
(6-d)²+6²+(6+d)² = 126
Simplifying:
(36-12d+d²)+36+(36+12d+d²) = 126
36-12d+d²+36+36+12d+d² = 126
2d²+108 = 126
Divide through by 2
d²+54 = 63
d² = 9
d = ±3
If d = +3, the three terms are, since a = 6
a-d = 6-3 = 3
a = 6
a+d = 6+3 = 9
If d = -3, the three terms are, since a = 6
a-d = 6-(-3) = 6+3 = 9
a = 6
a+d = 6+(-3) = 6-3 = 3
find the smallest number of the arithmetic progression
So regardless of whether the the numbers are
3,6,9 or 9,6,3,
The smallest is 3.
Edwin
|
|
|