Question 997811: The sum of three numbers in a.p is 12 and the sum of their squares is 66. what are the numbers
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be a middle number, then the first one is x-d and the third one is x+d, where d is the common difference.
The sum of three is 12. It means that
(x-d) + x + (x+d) = 12, or
3x = 12, x =  = 4. = 4.
The sum of squares is 66. It means that
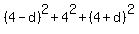 = = 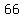 , or , or
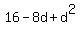 + +  + + 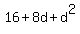 = = 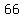 , ,
 + +  = = 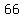 , ,
 = = 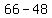 , ,
 = =  , ,
 = = 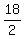 = =  , d = +/- , d = +/- . .
Thus our progression is 1, 4, 7 or 7, 4, 1.
|
|
|