SOLUTION: Find the 9th term of the harmonic sequence 3/2,1/2,3/10,3/14,... n=9

Algebra ->  Sequences-and-series -> SOLUTION: Find the 9th term of the harmonic sequence 3/2,1/2,3/10,3/14,... n=9      Log On


   

Question 983173: Find the 9th term of the harmonic sequence
3/2,1/2,3/10,3/14,... n=9
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Find the 9th term of the harmonic sequence
3%2F2,1%2F2,3%2F10,3%2F14,... n=9
Get their reciprocals:

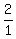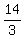2%2F3,2%2F1,10%2F3,14%2F3,... n=9

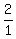If we write the 2%2F1 with a 3 denominator, as 6%2F3

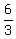we can see the arithmetic sequence which the reciprocals form:

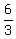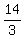2%2F3,6%2F3,10%2F3,14%2F3,... n=9

Extend it to 9 terms by adding common ratio 4%2F3 each time:

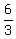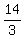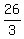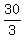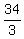2%2F3,6%2F3,10%2F3,14%2F3,18%2F3,22%2F3,26%2F3,30%2F3,34%2F3

Reduce all the fraction that will reduce:

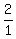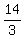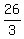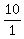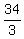2%2F3,2%2F1,10%2F3,14%2F3,6%2F1,22%2F3,26%2F3,10%2F1,34%2F3

Take the reciprocals:

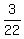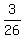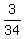3%2F2,1%2F2,3%2F10,3%2F14,1%2F6,3%2F22,3%2F26,1%2F10,3%2F34

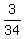9th term is 3%2F34

Edwin