SOLUTION: Given a4=35 and s14=931, find the common difference d and a1.

Algebra ->  Sequences-and-series -> SOLUTION: Given a4=35 and s14=931, find the common difference d and a1.      Log On


   

Question 978276: Given a4=35 and s14=931, find the common difference d and a1.
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
[You did not give enough information.  You had this:
an=35 and s14=931 a sub n ,common diffence and a sub 1
However I guessed that a4=35 was given, and rewrote your question as above.]

We use the nth term formula:

a%5Bn%5D%22%22=%22%22a%5B1%5D%2B%28n-1%29d

Substitute n=4, then a4=35

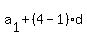
a%5B4%5D%22%22=%22%22a%5B1%5D%2B%284-1%29d

35%22%22=%22%22a%5B1%5D%2B3d

We use the sum formula:

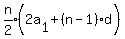S%5Bn%5D%22%22=%22%22expr%28n%2F2%29%282a%5B1%5D%2B%28n-1%29d%5E%22%22%29

Substitute n=14, then S14=931

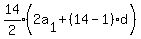
S%5B14%5D%22%22=%22%22expr%2814%2F2%29%282a%5B1%5D%2B%2814-1%29d%5E%22%22%29

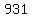
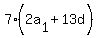931%22%22=%22%227%282a%5B1%5D%2B13d%5E%22%22%29

Both sides can be divided through by 7:

133%22%22=%22%222a%5B1%5D%2B13d%5E%22%22%29

So now we have this system of equations:

system%2835=a%5B1%5D%2B3d%2C133=2a%5B1%5D%2B13d%29

Solve that and get a1=8, d=8.

If my guess of a4=35 is correct, then your sequence was

8, 17, 26, 35, 44, 53, 62, 71, 80, 89, 98, 107, 116, 125 

That sequence of 14 terms does have sum 931.

If I guessed wrong, then you can use the above as a guide.

Edwin