Question 970169: What are the next two numbers in this series 1,8,27,58
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  , , , , , ,
first find the pattern:
To find the pattern, I will list the numbers, and find the differences for each pair of numbers. That is, I will subtract the numbers in pairs (the first from the second, the second from the third, and so on), like this:
 ......... ......... .......... .......... .......... .......... ..... .....
..... ......... ......... ......... .........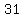 .... the "first differences", are not all the same value, I'll continue subtracting: .... the "first differences", are not all the same value, I'll continue subtracting:
.......... ......... ......... ....=> the second differences are the same, so the polynomial for this sequence of values is a quadratic ....=> the second differences are the same, so the polynomial for this sequence of values is a quadratic
Since the formula for the terms is a quadratic, then I know that it is of the form:
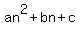 for some numbers for some numbers  , ,  , and , and 
Now I have to find those numbers by plugging in some of the values from the sequence, and then solving the resulting system of equations.
if  first term is first term is 

 ..........eq.1 ..........eq.1
if  second term is second term is 

 ..........eq.2 ..........eq.2
if  third term is third term is 

 ..........eq.3 ..........eq.3
start with
 ..........eq.2 ..........eq.2
 ..........eq.1 ..........eq.1
--------------------------------subtract
 --------solve for --------solve for 
 .........................(1) .........................(1)
now use
 ..........eq.3 ..........eq.3
 ..........eq.2 ..........eq.2
--------------------------------subtract
 --------solve for --------solve for 
 .........................(2) .........................(2)
use (1) and (2) to find 




now find 
 .........................(1) .........................(1)



go to eq.1 substitute  and and  , and find , and find 
 ..........eq.1 ..........eq.1




so, your polynomial,or nth term formula is:
 .......(for all terms given) .......(for all terms given)
now use formula to find the next two numbers in this series:






so, with these terms, your sequence is:  , , , , , , , , , ,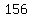
|
|
|