SOLUTION: If in a geometric progression,the second term exceeds the first term by 20 and the fourth term exceeds the second term by 15,find the possible values of the first term.

Algebra ->  Sequences-and-series -> SOLUTION: If in a geometric progression,the second term exceeds the first term by 20 and the fourth term exceeds the second term by 15,find the possible values of the first term.      Log On


   

Question 970124: If in a geometric progression,the second term exceeds the first term by 20 and the fourth term exceeds the second term by 15,find the possible values of the first term.
Answer by reviewermath(1029) About Me  (Show Source):
You can put this solution on YOUR website!
If in a geometric progression,the second term exceeds the first term by 20 and the fourth term exceeds the second term by 15,find the possible values of the first term.
Solution:
Let x = first term of a geometric progression and r = common ratio.
The terms of a geometric progression in terms of x and r are
x, xr, 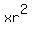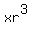xr%5E2, xr%5E3, ...
Therefore,
xr - x = 20 and 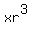xr%5E3 - xr = 15
x+=+20%2F%28r-1%29 and x+=+15%2F%28r%5E3-r%29
20%2F%28r-1%29+=+15%2F%28r%5E3-r%29
20%28r%5E3-r%29+=+15%28r-1%29
20r%5E3-35r%2B15=0
5(r-1)(2r-1)(2r+3) = 0
r = 1, 1/2, -3/2
If r = 1, then x is undefined
If r = 1/2, then x= 20%2F%281%2F2-1%29+=+-40
If r = -3/2, then x = 20%2F%28-3%2F2-1%29+=+-8
Answer: -40 or -8