Question 969778: Find the 1st term of this geometric sequence - 3 , 17
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! We need more information than that.
Is 3 the second term, and 17 the third term?
If it is a geometric sequence, then each term is the one before times a fixed number,  .
That number is called the common ratio, because it is the ratio between any two consecutive terms.
So, term number  ,  ,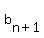
is related to the previous term,
term number  = ,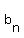
by  <--->
for all natural number (counting number) values of .
IF 3 and 17 are consecutive terms,
then the common ratio between consecutive terms is
 .
Each term is  times the one before.
IF 3 and 17 are the 2nd and 3rd terms respectively,
then  ,  , , and  is the first term that we want to find.
From , for  , we get
 ---> --->
so ---> ---> ---> --->
|
|
|
