SOLUTION: If a,b,c,d are in H.P., prove that a+d > b+c.

PROOF:
 
This is not true unless we rule out negative numbers.  For here is a 
counter-example:
 
, , ,   
 
are in H.P, because 8,5,2,-1 are in A.P. with common difference -3
 
yet  and  so a+d < b+c
 
So negative numbers cannot be allowed!
 
---------------
 
However it is true if a,b,c,d are all positive.  So you should point out 
to your teacher that the proposition is not true if you allow negative 
numbers.
 
So before we can prove the proposition, we must insert that requirement:

 
Then there exists positive numbers in A.P., x,x+y,x+2y,x+3y where x > 0
such that
 
, , , 

[Notice that although x is necessarily positive, y, the common difference, is
NOT NECESSARILY positive!  However a+d and b+c are positive]





Then



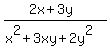is true because the numerators are the same positive number and the
denominator on the right is a larger positive number than the one
on the left.  Therefore  



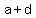
Edwin