If the first term is "a" and the difference is "d", then the first four terms
are
a, a+d, a+2d, a+3d
the sum of first four terms of an arithmetic sequence is 16
So,
a + a+d + a+2d + a+3d = 16
4a + 6d = 16
Divide thru by 2
2a + 3d = 8
their product 105,
So
a(a+d)(a+2d)(a+3d) = 105
So we have this system of two equations:
 Solve the first equation for "a":
2a = 8-3d
a =
Solve the first equation for "a":
2a = 8-3d
a = 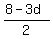 Substitute in the second equation:
Substitute in the second equation:

 Get LCD in each parentheses:
Get LCD in each parentheses:
 Combine fractions in parentheses:
Combine fractions in parentheses:

 Multiply both sides by 16
Multiply both sides by 16
 Rearrange the factors on the left:
Rearrange the factors on the left:
 FOIL
FOIL
 FOIL again:
FOIL again:
 Get 0 on the right side:
Get 0 on the right side:
 Get in descending order:
Get in descending order:
 Factor the trinomial:
Factor the trinomial:
 Factor further:
Factor further:

 ,
,  ,
, 
 ,
,  ,
, 



 We can ignore the irrational values for d, since the sequence
has only integers.
The only integer values for d are d=2 and d=-2
For d=2, substitute in
a =
We can ignore the irrational values for d, since the sequence
has only integers.
The only integer values for d are d=2 and d=-2
For d=2, substitute in
a = 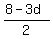 a =
a = 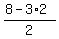 a =
a = 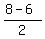 a =
a = 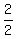 a =
a =  Substitute d=2 and a=1 in
a, a+d, a+2d, a+3d
1, 1+2, 1+2(2), 1+3(2)
Therefore 1 solution is
1, 3, 5, 7
----------------------------
For d=-2, substitute in
a =
Substitute d=2 and a=1 in
a, a+d, a+2d, a+3d
1, 1+2, 1+2(2), 1+3(2)
Therefore 1 solution is
1, 3, 5, 7
----------------------------
For d=-2, substitute in
a = 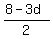 a =
a = 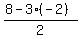 a =
a = 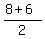 a =
a =  a =
a =  Substitute d=-2 and a=7 in
a, a+d, a+2d, a+3d
7, 7+(-2), 7+2(-2), 7+3(-2)
7, 5, 7-4, 7-6
Therefore another solution is
7, 5, 3, 1.
But this is the same sequence reversed.
Edwin
Substitute d=-2 and a=7 in
a, a+d, a+2d, a+3d
7, 7+(-2), 7+2(-2), 7+3(-2)
7, 5, 7-4, 7-6
Therefore another solution is
7, 5, 3, 1.
But this is the same sequence reversed.
Edwin