Question 953175: 3x-4;4x-2 and 7x-6 form an arithmetic sequence. Determine x and hence the three terms
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
If a sequence of values follows a pattern of adding a fixed amount from one term to the next, it is referred to as an arithmetic sequence. The number added to each term is constant (always the same).
The fixed amount is called the common difference,  , referring to the fact that the difference between two successive terms yields the constant value that was added.
To find the common difference, subtract the first term from the second term.
To find any term of an arithmetic sequence:
where  is the first term of the sequence, is the common difference, is the number of the term to find
since we have three terms 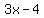 ,  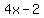,  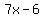, and common difference , substitute it in formula above:
so, your sequence is:
 =>
 =>
 =>
|
|
|
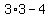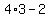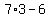