If we wanted to find the find the common ratio,
we would divide any term by the its preceding term.
Even though we don't care what the common ratio is,
we use this principle as though we did want to find
it:
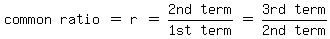
Creoss-multiply:
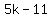
Use FOIL:
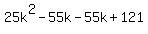
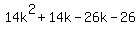
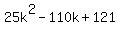
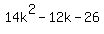
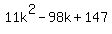
Factor
; 
; 
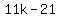
Those are the two possible values for k.
----------------------------------------------------------
If we wanted to find the three terms and the common ratio r,
we would substitute those values for k and find:
If k = 21/11, then the three terms would be 64/11, -16/11, 4/11,
with a common ratio r = -1/4
If k = 7, then the three terms would be 16, 24, 36,
with a common ratio r = 3/2
Edwin
