 ≟
≟  Prove true for n=1
Prove true for n=1
 = 4*1-1 = 4-1 = 3 and 1(2*1+1) = 1(3) = 3
So it is true for n=1
Assume it is true for some value k.
= 4*1-1 = 4-1 = 3 and 1(2*1+1) = 1(3) = 3
So it is true for n=1
Assume it is true for some value k.
 =
= 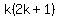 Add the next term 4(k+1)-1 to both sides:
Add the next term 4(k+1)-1 to both sides:
 =
= 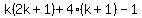
 =
= 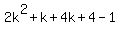
 =
= 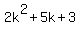
 = (k+1)(2k+3}
Now we show that the right side is the right side of
= (k+1)(2k+3}
Now we show that the right side is the right side of
 ≟ n(2n+1)
when k+1 is substituted for n.
≟ n(2n+1)
when k+1 is substituted for n.
 = (k+1)[2(k+1)+1] = (k+1)[2k+2+1) = (k+1)(2k+3)
So we have proved that IF it is true for any value of n, then it will
be true for the next value of n.
We have indeed proved that it is true for some value of n, namely 1, so
it will be true for the next value of n, which is 2.
Now since we have proved that IF it is true for any value of n, then it will
be true for the next value of n, and now since it is true for n=2, it will
be true for the next value of n which is 3.
And since it's true for n=3 it is true for n=4, etc. etc.
So it can never stop being true for any positive inbteger n.
So now we can erase the ? off the top of the = sign and get:
= (k+1)[2(k+1)+1] = (k+1)[2k+2+1) = (k+1)(2k+3)
So we have proved that IF it is true for any value of n, then it will
be true for the next value of n.
We have indeed proved that it is true for some value of n, namely 1, so
it will be true for the next value of n, which is 2.
Now since we have proved that IF it is true for any value of n, then it will
be true for the next value of n, and now since it is true for n=2, it will
be true for the next value of n which is 3.
And since it's true for n=3 it is true for n=4, etc. etc.
So it can never stop being true for any positive inbteger n.
So now we can erase the ? off the top of the = sign and get:
 =
=  Edwin
Edwin