Question 933333: If a,b,c,d are in H.P., prove that ab+bc+cd = 3ad
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a,b,c,d are in H.P., prove that ab+bc+cd = 3ad
Then the reciprocals  are in AP.
Let 2k = the common difference of the AP
Let m = the mean of the four terms of the AP
[Note: m is the number half-way between the middle two terms, so 1/b is k
less than m and 1/a is 2k less than 1/b or 3k less than m. Similarly 1/c
is k more than m and 1/d is 2k more than 1/c or 3k more than m.)
So are in AP.
Let 2k = the common difference of the AP
Let m = the mean of the four terms of the AP
[Note: m is the number half-way between the middle two terms, so 1/b is k
less than m and 1/a is 2k less than 1/b or 3k less than m. Similarly 1/c
is k more than m and 1/d is 2k more than 1/c or 3k more than m.)
So  , ,  , ,  , ,  and
and  , ,  , ,  , , 
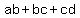  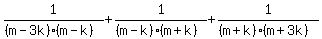  Get LCD:
Get LCD:
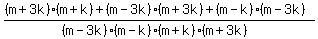 
 
 
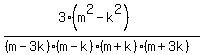 
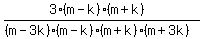 
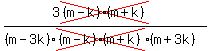 
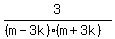 
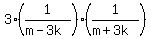 
 Edwin
Edwin
|
|
|