SOLUTION: A series of 384 consecutive odd integers has a sum that is a perfect fourth power of a positive integer. Find the smallest possible sum for this series. a) 104 976 b) 20 736 c

Let the first odd integer be 2k-1 where k is an integer

The sum of an arithmetic series is



With odd integers d=2, we'll let a1 = 2k-1, n=384















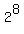 is a perfect 4th power. Since we have one factor of 3,

the smallest 4th power possible will be .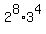

That's the answer: 

, choice b

---------

Following through,

This will be when  



Notice that the problem just said "consecutive odd integers", it didn't
say they had to be positive!

So the sequence of 384 odd integers starts with 2k-1 = 2(-164)-1 = -329

and ends with 

So it's the series of 384 consecutive odd integers

(-329)+(-327)+...+435+437 = 20736 = 124

Edwin