In a geometric series, the sum of the first three terms is 304,
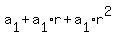
(1) 
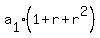
and the sum of the first six terms is 1330.
So the sum of the 3rd, 4th and 5th terms only is 1330-304 = 1026
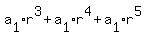
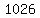(2) 
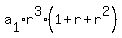
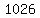Dividing equals by equals, equation (2) by equation (1)
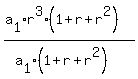
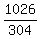
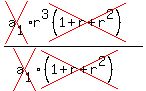
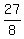
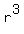
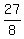Taking cube roots of both sides
Substitute in equation (1)
(1)
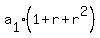
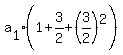
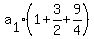
Multiply the terms in the parentheses and the right side by 4
to clear of fractions:
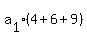
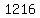
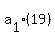
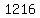Divide both sides by 19
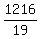
Find the sum of the first seven terms.
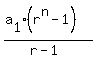
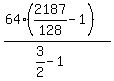Multiply the top out, the 16 goes into the 128 2 times,
and write the 1 on the bottom as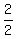 
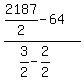
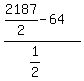Multiply top and bottom by 2
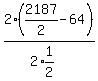
Edwin
