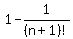SOLUTION: show that 1/2!+2/3!+3/4!+...+n/(n+1)!=1-1/(n+1)!. where n!=1*2*3*...*n. note:*=multiply

First we prove that when n=1, and there is just 1 term on the left,
the the above is true:



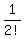
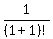That is true since 1+1=2

Now since we have a value of n where it works, we can assume that
there is at least one value of n=k where it works, for we know it
works for k=1 as we just showed.

So we can be sure that there is at least one value of k where



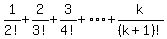
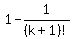is true, even if it were only true only for k=1.

Now we will add the next term 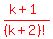 to both sides:



                              

                              

                              

                              

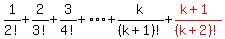
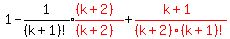
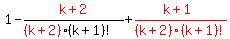
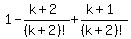Notice there is a "-" before the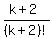 

                              

                              

                              



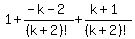
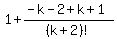
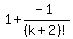
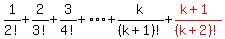
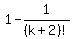That's the formula with n equaling to k+1

So we have shown that if the formula works for some n=k, then it works 
also for n=k+1

Therefore since we have shown that it works for n=k=1, this proves that it
also works for n=k=2.
Therefore since we have shown that it works for n=k=2, this proves that it
also works for n=k=3.
Therefore since we have shown that it works for n=k=3, this proves that it
also works for n=k=4.

etc. etc.

So it works for ALL values of n

Edwin