Question 874586: what is the pattern in this sequence: 1, 10, 25, 55, 109, 196, and 325
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The differences between consecutive terms are
9, 15, 30, 54, 87, 129.
If they were the same, it would be an arithmetic sequence,
and calling the initial term  , and the common difference  ,
term number  would be
 .
In other words, 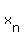 would be a linear function of .
The differences of the differences are
If those differences were the same, 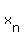would be a quadratic function of .
The differences of the differences of the differences are all  :
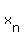must be a cubic function of .
From the differences, we can make a table and figure out that the next terms are
505, 745, 1054.
The table would be
Finding a formula is a little harder.
The fact that the third differences are constant means that 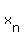is a cubic function of
 -->
 --> --> -->
 --> --> -->
Solving  we find can find the formula easily enough:
From ,
subtracting the first equation from the other two we get
Subtracting 2 times  , or  , from  we get
 --> --> --> -->
The formula is 
We already know that it will give us
 ,  ,  , and  ,
because we used those terms to find the coefficients.
Using the formula found for the next given terms, we see that it works:
|
|
|
