Question 872714: 6 , 13 , 25 , 52 , 101 , ?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! 6 , 13 , 25 , 52 , 101 ,
The method I show below will always work for any sequence. However
it may not be the answer your teacher wants. If your teacher
wants a different answer, then he or she should tell you what
sort of answer you are to give, because sequence problems always
have many possible different patterns for the nth terms which
work for any finite number of given terms. It is a bit much for
a teacher to expect a student to try out thousands of possible
nth terms all which work for the given terms in order to come up
with the "simplest" one. Teachers do not have to come up
with the simplest one themselves, for they already have the answer
from the source from which they got the sequence. It is just not
fair for teachers to ask students to do something that they
themselves cannot do. MY opinion!
That being said, the nth term which works for the given sequence,
I got by assuming an nth term of the form
   and substituting n=1,2,3,4,5 and
and substituting n=1,2,3,4,5 and  =6,13,25,52,12
I got: =6,13,25,52,12
I got:
 , ,  , ,  , ,  , ,  Which gives:
Which gives:
   Gettng a common denominator of 24, that becomes
Gettng a common denominator of 24, that becomes
  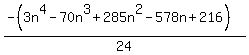 To prove that this nth term works:
Substituting n = 1:
To prove that this nth term works:
Substituting n = 1:
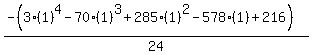
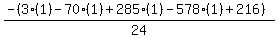
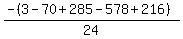
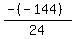

 Substituting n = 2:
Substituting n = 2:
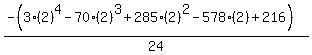

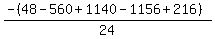
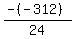

 Substituting n = 3:
Substituting n = 3:
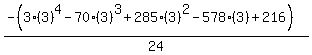
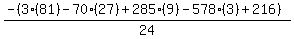
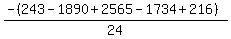
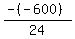
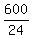
 Substituting n = 4:
Substituting n = 4:
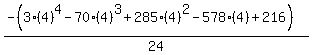
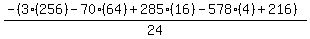
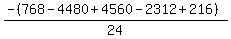
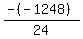

 Substituting n = 5:
Substituting n = 5:
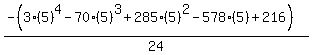

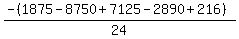
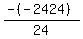

 Substituting n = 6:
Substituting n = 6:
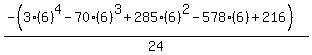
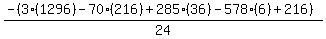

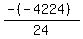

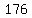 Substituting n = 7:
Substituting n = 7:
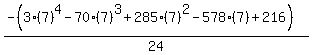
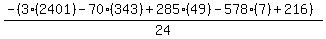
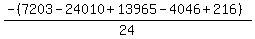


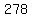 Substituting n = 8:
Substituting n = 8:
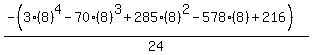
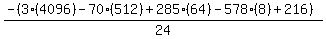
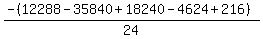


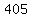 Substituting n = 9:
Substituting n = 9:
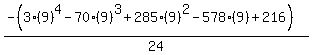
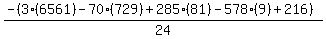
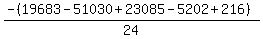


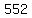 Substituting n = 10:
Substituting n = 10:
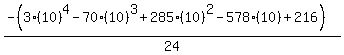
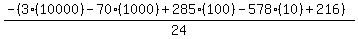



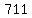 Substituting n = 11:
Substituting n = 11:

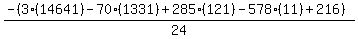

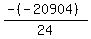

 Substituting n = 12:
Substituting n = 12:
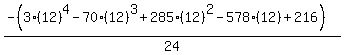
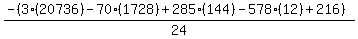
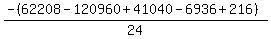
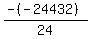

 Substituting n = 13:
Substituting n = 13:
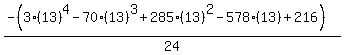


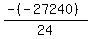

 Substituting n = 14:
Substituting n = 14:
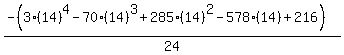
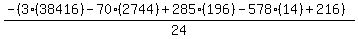
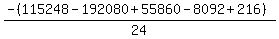


 Substituting n = 15:
Substituting n = 15:

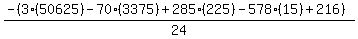
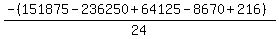


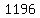 Substituting n = 16:
Substituting n = 16:
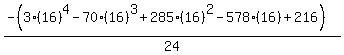
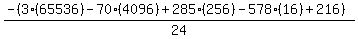
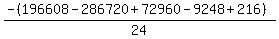


 Substituting n = 17:
Substituting n = 17:
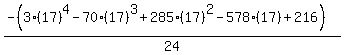
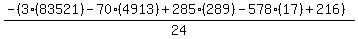
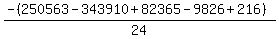
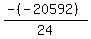

 Substituting n = 18:
Substituting n = 18:
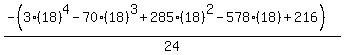
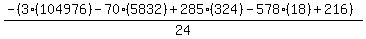
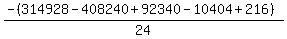
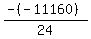

 Substituting n = 19:
Substituting n = 19:
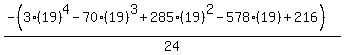
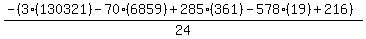
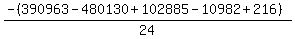
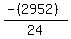

 Substituting n = 20:
Substituting n = 20:
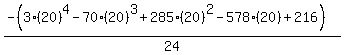
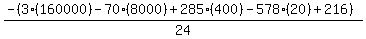
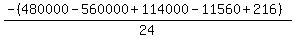
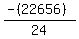

 Edwin
Edwin
|
|
|