Question 87164: Use the geometric sequence of numbers 1, 3, 9, 27
to find the following:
a) What is r, the ratio between 2 consecutive terms?
Answer: r =3
Show work in this space.
1*3=3 3*3=9 3*9=27 ECT
b) Using the formula for the nth term of a geometric sequence, what is the 10th term?
Answer:
Show work in this space.
Use the geometric sequence of numbers 1, 1/3, 1/9, 1/27
to find the following:
a)What is r, the ratio between 2 consecutive terms?
Answer:
Show work in this space.
b)Using the formula for the sum of the first n terms of a geometric sequence, what is the sum of the first 10 terms? Carry all calculations to 6 decimals on all assignments.
Answer:
Show work in this space.
c)Using the formula for the sum of the first n terms of a geometric sequence, what is the sum of the first 12 terms? Carry all calculations to 6 decimals on all assignments.
Answer:
Show work in this space.
d) What observation can make about the successive partial sums of this sequence? In particular, what number does it appear that the sum will always be smaller than?
Answer:
I really need help on these problems. I am at a total lose here. Please Help me out. Thank you!
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem #1
"Use the geometric sequence of numbers 1, 3, 9, 27
to find the following:"
a)
The ratio r is the factor to get from term to term. So to find r, simply pick any term and divide it by the previous term:
 Divide the term of 27 by 9 Divide the term of 27 by 9
So the ratio is

b)
The sequence is multiplying by a factor of 3 each term, so the sequence is 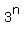
This means the 10th term is
 (let n=9, remember n=0 is the 1st term) (let n=9, remember n=0 is the 1st term)
So the 10th term is 19,683
---------------------------------------------------------
Problem #2
"Use the geometric sequence of numbers 1, 1/3, 1/9, 1/27
to find the following:"
a)
The ratio r is the factor to get from term to term. So to find r, simply pick any term and divide it by the previous term:
 Divide the term of Divide the term of 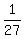 by by 
So the ratio is

The sequence is reduced by a factor of  each term, so the sequence is each term, so the sequence is 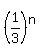
b)
The sum of a geometric series is
 where a=1 where a=1
 So plug in So plug in  and n=10 to find the sum of the first 10 partial sums and n=10 to find the sum of the first 10 partial sums
 Raise Raise  to the 10 power to the 10 power
 Make "1" into an equivalent fraction with a denominator of 59049 Make "1" into an equivalent fraction with a denominator of 59049
 Subtract the fractions in the numerator Subtract the fractions in the numerator
 Subtract the fractions in the denominator Subtract the fractions in the denominator
 Flip the 2nd fraction, multiply, and simplify Flip the 2nd fraction, multiply, and simplify
So the sum of the first ten terms is 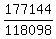 or 1.49997459736829 approximately or 1.49997459736829 approximately
note: I chose to use fractions (to maintain accuracy), but it may be much easier for you to simply use a calculator to evaluate the sum.
c)
The sum of a geometric series is
 where a=1 where a=1
 So plug in So plug in  and n=12 to find the sum of the first 12 partial sums and n=12 to find the sum of the first 12 partial sums
 Raise Raise  to the 10 power to the 10 power
 Make "1" into an equivalent fraction with a denominator of 531441 Make "1" into an equivalent fraction with a denominator of 531441
 Subtract the fractions in the numerator Subtract the fractions in the numerator
 Subtract the fractions in the denominator Subtract the fractions in the denominator
 Flip the 2nd fraction, multiply, and simplify Flip the 2nd fraction, multiply, and simplify
So the sum of the first twelve terms is 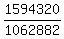 or 1.49999717748537 approximately or 1.49999717748537 approximately
d)
It appears that the sums are approaching a finite number of  or 1.5. This is because each term is getting smaller and smaller. This observation is justified by the fact that if or 1.5. This is because each term is getting smaller and smaller. This observation is justified by the fact that if 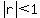 then the infinite series will approach a finite number. In other words then the infinite series will approach a finite number. In other words
If 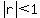 (the magnitude of r has to be less than 1) then, (the magnitude of r has to be less than 1) then,
 Where S is the sum of the infinite series. So if we let a=1 and r=1/3 we get Where S is the sum of the infinite series. So if we let a=1 and r=1/3 we get


 So this verifies that our series approaches So this verifies that our series approaches  . .
|
|
|