Question 871381: A recursive formula for the following series: 1, 3/2, 5/6, 7/24, 9/120
Found 2 solutions by KMST, richwmiller:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A recursive formula shows how to get the next term from the one before, to 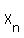 from from 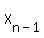 . .
I know the idea to get 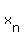 from from 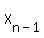 . .
From the terms you are given, in the form given,
to get term number  , ,
you add 2 to the numerator and multiply the denominator by  . .
So for the 6th term, you take 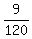 ; ;
change the numerator from  to to  , ,
and change the denominator from  to to  , ,
to get  . .
However, if I was given 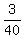 as a term, how would I know that as a term, how would I know that  , ,
and how would I know that  is the fifth term. is the fifth term.
It is not so easy.
I could do it, but I do not know how to write it as a recursive formula..
I do see an explicit formula to calculate term number  from from  , not counting on term number , not counting on term number 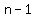 ) . ) .






If you only told me that one of the terms is 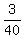 , ,
I would factor  as as  . .
I would multiply numerator and denominator times  , ,
to have  as a denominator. as a denominator.
Then, suspecting that  is term number is term number  , ,
I would verify that with  as denominator, the numerator is as denominator, the numerator is  . .
After that, from 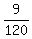 , ,
I would change the numerator from  to to  , ,
and change the denominator from  to to  , ,
to get  . .
I cannot write that as a recursive formula,
but since no one else answered your question before,
I assume that not many people can.
Answer by richwmiller(17219)   (Show Source): (Show Source):
|
|
|