Determine the sum of the natural numbers less than 100 which are not multiples of 5
First we'll find the sum of the natural numbers less than 100.
Then we'll find the sum of the multiples of 5.
Then we'll subtract the second sum from the first sum.
The natural numbers less that 100 is an arithmetic sequence
1,2,3,...,99
with a1 = 1 and an = 99, and n = 99.
The formula is:
Sn =  (a1 + an)
Sn =
(a1 + an)
Sn = 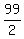 (1 + 99)
Sn =
(1 + 99)
Sn = 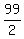 (100)
Sn =
(100)
Sn =  = 4950
The sequence of multiples of 5 less that 100 are 5,10,15,...,95
That's an arithmetic sequence with a1 = 5 and an = 99. To find n for this sequence we use:
an = a1 + (n-1)d
with a1 = 5 and an = 95 and d=5
95 = 5 + (n-1)5
95 = 5 + 5n - 5
95 = 5n
19 = n
Use the same sum formula:
Sn =
= 4950
The sequence of multiples of 5 less that 100 are 5,10,15,...,95
That's an arithmetic sequence with a1 = 5 and an = 99. To find n for this sequence we use:
an = a1 + (n-1)d
with a1 = 5 and an = 95 and d=5
95 = 5 + (n-1)5
95 = 5 + 5n - 5
95 = 5n
19 = n
Use the same sum formula:
Sn =  (a1 + an)
S19 =
(a1 + an)
S19 = 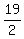 (5 + 95) =
(5 + 95) = 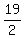 = 19×50 = 950
Then we subtract: 4950 - 950 = 4000
Edwin
= 19×50 = 950
Then we subtract: 4950 - 950 = 4000
Edwin