Each term of sequence is determined by adding half to the preceding term.The sum of the first twenty five terms of the sequence equals the square of the twenty fifth term. How can I calculate the possible value of the first term?
Substitute d=0.5 and n=25 in the formula for the nth term
of an arithmetic sequence.
an = a1 + (n-1)d
a25 = a1 + (25-1)(.5)
a25 = a1 + (24)(.5)
a25 = a1 + 12
Substitute the same values d=0.5 and n=25 in the formula
for the sum of the first n terms of an arithmetic sequence.
Sn = 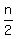 [2a1 + (n-1)d]
S25 =
[2a1 + (n-1)d]
S25 = 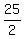 [2a1 + (25-1)(.5)]
S25 =
[2a1 + (25-1)(.5)]
S25 = 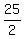 [2a1 + (24)(.5)]
S25 =
[2a1 + (24)(.5)]
S25 = 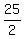 [2a1 + 12]
S25 = 25a1 + 150
[2a1 + 12]
S25 = 25a1 + 150
The sum of the first twenty five terms of the sequence equals the square of the twenty fifth term
So
S25 = (a25)²
25a1 + 150 = (a1 + 12)²
25a1 + 150 = (a1)² + 24a1 + 144
0 = (a1)² - a1 - 6
0 = (a1 + 2)(a1 - 3)
a1 + 2 = 0; a1 - 3 = 0
a1 = -2; a1 = 3
So there are two solutions for the first term, -2 and 3
Checking both by computer, gave these lists of 25 terms and
the sums all the way to the 25th term:
1. term = -2 , sum = -2 1. term = 3 , sum = 3
2. term = -1.5 , sum = -3.5 2. term = 3.5 , sum = 6.5
3. term = -1 , sum = -4.5 3. term = 4 , sum = 10.5
4. term = -0.5 , sum = -5 4. term = 4.5 , sum = 15
5. term = 0 , sum = -5 5. term = 5 , sum = 20
6. term = 0.5 , sum = -4.5 6. term = 5.5 , sum = 25.5
7. term = 1 , sum = -3.5 7. term = 6 , sum = 31.5
8. term = 1.5 , sum = -2 8. term = 6.5 , sum = 38
9. term = 2 , sum = 0 9. term = 7 , sum = 45
10. term = 2.5 , sum = 2.5 10. term = 7.5 , sum = 52.5
11. term = 3 , sum = 5.5 11. term = 8 , sum = 60.5
12. term = 3.5 , sum = 9 12. term = 8.5 , sum = 69
13. term = 4 , sum = 13 13. term = 9 , sum = 78
14. term = 4.5 , sum = 17.5 14. term = 9.5 , sum = 87.5
15. term = 5 , sum = 22.5 15. term = 10 , sum = 97.5
16. term = 5.5 , sum = 28 16. term = 10.5 , sum = 108
17. term = 6 , sum = 34 17. term = 11 , sum = 119
18. term = 6.5 , sum = 40.5 18. term = 11.5 , sum = 130.5
19. term = 7 , sum = 47.5 19. term = 12 , sum = 142.5
20. term = 7.5 , sum = 55 20. term = 12.5 , sum = 155
21. term = 8 , sum = 63 21. term = 13 , sum = 168
22. term = 8.5 , sum = 71.5 22. term = 13.5 , sum = 181.5
23. term = 9 , sum = 80.5 23. term = 14 , sum = 195.5
24. term = 9.5 , sum = 90 24. term = 14.5 , sum = 210
25. term = 10 , sum = 100 25. term = 15 , sum = 225
Using a1 = -2, a25 = 10, S25 = 100 which is 10².
Using a1 = 3, a25 = 15, S25 = 225 which is 15².
Edwin