SOLUTION: The first two terms of a geometric sequence and an arithmetic sequence are the same. The first term is 12. The sum of the first three terms of the geometric sequence is 3 more than

Algebra ->  Sequences-and-series -> SOLUTION: The first two terms of a geometric sequence and an arithmetic sequence are the same. The first term is 12. The sum of the first three terms of the geometric sequence is 3 more than      Log On


   

Question 840912: The first two terms of a geometric sequence and an arithmetic sequence are the same. The first term is 12. The sum of the first three terms of the geometric sequence is 3 more than the sum of the first three terms of the arithmetic sequence. Determine TWO possible values for the common ratio, r, of the geometric sequence
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The first two terms of a geometric sequence and an arithmetic sequence are the same. The first term is 12. The sum of the first three terms of the geometric sequence is 3 more than the sum of the first three terms of the arithmetic sequence. Determine TWO possible values for the common ratio, r, of the geometric sequence
Geometric sequence = a,ar,arē,__,__,...

Arithmetic sequence= a,a+d,a+2d,__,__,...
The first two terms of a geometric sequence and an arithmetic sequence are the same.
a = a, ar = a+d

The first term is 12. 

a = 12,  12r = 12+d
The sum of the first three terms of the geometric sequence is 3 more than the sum of the first three terms of the arithmetic sequence.
   (a)+(ar)+(arē) = (a)+(a+d)+(a+2d)+3
(12)+(12r)+(12rē) = (12)+(12+d)+(12+2d)+3
      12+12r+12rē = 12+12+d+12+2d+3
      12+12r+12rē = 39+3d
         12r+12rē = 27+3d

Every term can be divided by 3

           4r+4rē = 9+d

So we have this system of two equations and 2 unknowns:

     12r = 12+d, 4r+4rē = 9+d

Solve the first for d:

         12r = 12+d     
      12r-12 = d

Substitute in

      4r+4rē = 9+d
      4r+4rē = 9+(12r-12)
      4r+4rē = 9+12r-12
      4r+4rē = 12r-3
    4rē-8r+3 = 0
(2r-1)(2r-3) = 0
   2r-1=0;  2r-3=0
     2r=1;    2r=3
      r=1%2F2;    r=3%2F2

Those are the two values.

---------------------------------------

To check we must find d

Using r = 1%2F2

 12r-12 = d
12%281%2F2%29-12 = d
   6-12 = d
     -6 = d

Arithmetic sequence:  12, 6, 0, ...
Geometric sequence:   12, 6, 3, ...

Sum of 1st three terms of arithmetic sequence = 12+6+0 = 18
Sum of 1st three terms of geometric sequence  = 12+6+3 = 21
21 is 3 more than 18
That checks.

Using r = 3%2F2

 12r-12 = d
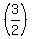12%283%2F2%29-12 = d
  18-12 = d
      6 = d

Arithmetic sequence:  12, 18, 24, ...
Geometric sequence:   12, 18, 27, ...

Sum of 1st three terms of arithmetic sequence = 12+18+24 = 54
Sum of 1st three terms of geometric sequence  = 12+18+27 = 57
57 is 3 more than 54
That checks, too.  So it's correct

Edwin