SOLUTION: Three positive numbers are in the ratio 1:3:8. if 7 is added to the largest number the three numbers form a geometric sequence. Find the numbers.

Algebra ->  Sequences-and-series -> SOLUTION: Three positive numbers are in the ratio 1:3:8. if 7 is added to the largest number the three numbers form a geometric sequence. Find the numbers.       Log On


   

Question 839221: Three positive numbers are in the ratio 1:3:8. if 7 is added to the largest number the three numbers form a geometric sequence. Find the numbers.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Since the numbers are in the ratio 1:3:8, then k:3k:8k where k is
not zero, represents all triples of numbers in the ration 1:3:8

So let the three numbers be k,3k, and 8k

Then the terms k, 3k, and 8k+7 form a geometric sequence.

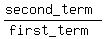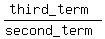The common ratio = %28second_term%29%2F%28first_term%29 = %28third_term%29%2F%28second_term%29

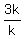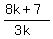
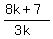Therefore  3k%2Fk = %288k%2B7%29%2F%283k%29
           3 = %288k%2B7%29%2F%283k%29
Multiply through by 3k  
            
           9k = 8k+7
            k = 7

Then the numbers are  k,3k, and 8k or 7,21,56

Checking: adding 7 to the 3rd term gives the sequence 7,21,63

That checks, since 7*3=21 and 21*3=63

Edwin