1,4,3,6,5,8, ____?
Notice that the odd terms are 1,_,3,_,5,_
(and that the even terms are _,4,_,6,_,8)
The odd terms are the same as the odd terms of the sequence
1,2,3,4,5,6,... which has general term n
Subtracting this sequence term by term from the given sequence:
{1,4,3,6,5,8,...
-{1,2,3,4,5,6,...
---------------
0,2,0,2,0,2,...
That sequence of differences has general term 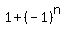 Since the opposite of the above subtraction is this addition:
{1,2,3,4,5,6,... which has general term n
+{0,2,0,2,0,2,... which has general term
Since the opposite of the above subtraction is this addition:
{1,2,3,4,5,6,... which has general term n
+{0,2,0,2,0,2,... which has general term 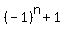 , so
---------------
1,4,3,6,5,8,...
the given sequence has the general term
, so
---------------
1,4,3,6,5,8,...
the given sequence has the general term 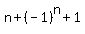 . It goes:
1,4,3,6,5,8,7,10,9,12,11,14,13,...
----------------------------------------
Note:
You could also look at the given sequence as this sequence but
without the first term 2:
2,1,4,3,6,5,8,7,10,9,12,11,14,13,
You start with the sequence
1,2,3,4,5,6,7,8,9,10,11,12,13,14,...
and swap every odd number with the next higher even number.
But your sequence doesn't have the 2 as its first term, but
starts with the 1 instead.
Edwin
. It goes:
1,4,3,6,5,8,7,10,9,12,11,14,13,...
----------------------------------------
Note:
You could also look at the given sequence as this sequence but
without the first term 2:
2,1,4,3,6,5,8,7,10,9,12,11,14,13,
You start with the sequence
1,2,3,4,5,6,7,8,9,10,11,12,13,14,...
and swap every odd number with the next higher even number.
But your sequence doesn't have the 2 as its first term, but
starts with the 1 instead.
Edwin