The odd numbered terms form the arithmetic 1,29,57 with common difference 28.
So if we used only half that difference, 14, we would have the arithmetic
sequence 1,15,29,43,57, which has the same odd-numbered terms but different
even-numbered terms. The nth term of that sequence is
 Let's compare the sequences and observe how the even numbered terms
of this sequence differ from the even numbered terms of the given sequence:
This sequence: 1,15,29,43,57 (arithmetic sequence, nth term 14n-13)
Given sequence: 1, 7,29,51,57
-----------------------------------
Difference sequence: 0, 8, 0,-8, 0
So if we can think of a sequence that goes 0,8,0,-8,0,8,0,-8, ...
we can add it to the arithmetic sequence and we'll have the
nth term of your sequence. Those are the x-intercept, maximum,
x-intercept, minimum, x-intercept,...
of the sine curve with amplitude 8
Let's compare the sequences and observe how the even numbered terms
of this sequence differ from the even numbered terms of the given sequence:
This sequence: 1,15,29,43,57 (arithmetic sequence, nth term 14n-13)
Given sequence: 1, 7,29,51,57
-----------------------------------
Difference sequence: 0, 8, 0,-8, 0
So if we can think of a sequence that goes 0,8,0,-8,0,8,0,-8, ...
we can add it to the arithmetic sequence and we'll have the
nth term of your sequence. Those are the x-intercept, maximum,
x-intercept, minimum, x-intercept,...
of the sine curve with amplitude 8
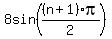 So the nth term is
So the nth term is


 .
That sequence is 1,7,29,51,57,63,85,107,113,...
Edwin
.
That sequence is 1,7,29,51,57,63,85,107,113,...
Edwin