SOLUTION: The 11th term of an arithmetic sequence is 57 and the sum of the first and the fourth terms is 29.Determine the first 3 terms of the sequence. . .please help me step by step

a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11

You need this formula for the nth term:

an = a1 + (n-1)d

[Some books and teachers use "t" for "term" instead of "a".
I'll use "a".]

a11 = a1 + (11-1)d
57 = a1 + 10d

a1 + a4 = 29

Substitute n=4 in the formula also

a4 = a1 + (4-1)d
a4 = a1 + 3d

Now substitute for a4 in 

a1 + a4 = 29

a1 + (a1 + 3d) = 29 

a1 + a1 + 3d = 29

2a1 + 3d = 29

So you have this system of equations:

57 = a1 + 10d
2a1 + 3d = 29

Solve the first for a1

57-10d = a1

Substitute in 

2a1 + 3d = 29
2(57-10d) + 3d = 29
114 - 20d + 3d = 29
     114 - 17d = 29
          -17d = -85
             d =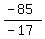 
             d = 5

Substitute d=5 in 

57-10d = a1
57-10(5) = a1
57-50 = a1
7 = a1

So the sequence starts with a1=7 and adds d=5 each time.

To check, let's write them all out and see if the llth terms comes out
to be 57. 

7, 12, 17, 22, 27, 32, 37, 42, 47, 52, 57

The last one came out 57.  Count them.  There are 11.  So it's correct. 

7, 12, 17

Edwin