 This is not true!
Although equality holds for n=1:
This is not true!
Although equality holds for n=1:



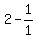

 It isn't true for n=2 or greater, for when n=2
It isn't true for n=2 or greater, for when n=2
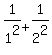

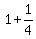

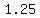 yet
yet


 ,
,  holds but not
holds but not  And when n=3
And when n=3
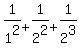

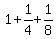

 yet
yet


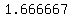 , again
, again  holds but not
holds but not  .
Euler proved in 1735 that the the sum on the left approaches the irrational
number
.
Euler proved in 1735 that the the sum on the left approaches the irrational
number 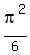 = 1.6449340668482264... and it is an increasing function, so it
is always less that
= 1.6449340668482264... and it is an increasing function, so it
is always less that 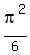 .
The expression on the right is also increasing, and approaches 2. But
beginning with the third term it is already larger than the left side can
ever be!
Edwin
.
The expression on the right is also increasing, and approaches 2. But
beginning with the third term it is already larger than the left side can
ever be!
Edwin