Question 796191: How many terms of the arithmetic progression 24,22,20 are needed to give the sum of 150?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE MENTAL MATH WAY:
The sum of an arithmetic progression is the average of the first and last terms times the number of therms.
If we add all the numbers between  and and  , we would be adding 12 terms, and multiplying times 12 is not easy. , we would be adding 12 terms, and multiplying times 12 is not easy.
Leaving out 2, and 4, I would have just 10 terms, and
24+22+20+ ,,, +10+8+6 =
So adding  we get 150. we get 150.
WITH FORMULAS
That progression has a first term

and a common difference 
The sum of the first  terms of an arithmetic progression can be calculated as terms of an arithmetic progression can be calculated as
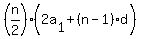
In this case that sum would be 150, so







 --> --> 
Adding the 10 terms 24+22+ ... +10+8+6,
or adding the 15 terms 24+22+ ... +10+8+6 +4+2+0-2-4
we get 150,
but I would say  terms are needed to get to 150. terms are needed to get to 150.
There is no need to keep adding 4+2+0+(-2)+(-4)=0.
|
|
|