Question 741827: Is there a formula to solve this question....The population of a community was 82,000 at the beginning of 2000. Assuming a rate of growth of 1.6% per year since 2000, what will be the population be at the beginning of 2025?
I can manually get the answer but would rather use a formula. Is there one that will work? I can't seem to get the formulas that I know to work.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  = years since the beginning of 2000
At the beginning of 2000,  and the population is
At the beginning of 2001, 1 year has passed and the population has increased by 1.6%,
meaning that the increase is  of the initial amount,
so it has increased by 
That means that at the beginning of 2001, when  , the population is
With numbers it would be 
That number is not important. What's important is that the population number got multiplied times  .
With the passage of each year the population gets increased (multiplied) by a factor of  .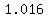
After 2 years, it would have been multiplied by 1.016 again, and it would be  .
After 3 years, it would have been multiplied by 1.016 again, and it would be  , and so on.
If you are studying sequences and series, your teacher would say that it is a geometric sequence with a common ratio of .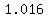
After years the population will be  .
Using your initial population of 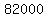 at the beginning of 2000, it is
At the beginning of 2025,  and my calculator says that
 (rounded)
NOTE: That kind of growth is called exponential growth.
If you use the growth factor per unit of time in the formula, the time will be the exponent.
In mathematics they like to use powers of the irrational number  instead, so you see formulas like
 , but if you do not know about and natural logarithms, don't worry about it, because I do not think that would help your calculation at all.
|
|
|
