|
Question 740508: Determine the common ratio of a geometric series that has these partial sums: S4= -3.5, S5= -3.75, S6= -3.875.
I am having a lot of problems trying to find the common ratio. This is a multiple question and none of the answers fit.
Found 3 solutions by Ed Parker, lynnlo, ikleyn:
Answer by Ed Parker(21)   (Show Source): (Show Source):
You can put this solution on YOUR website!
S4= -3.5, S5= -3.75, S6= -3.875.
The sum of the first 5 terms S5 minus the sum
of the first 4 terms S4 is the fifth term a5.
That is:
-3.75 = S5 = a1+a2+a3+a4+a5
-3.5 = S4 = a1+a2+a3+a4
-----------------------------------
Subtract those equations term by term
-3.75 - (-3.5) = a5
-3.75 + 3.5 = a5
-0.25 = a5
------------------------------------
Similarly, the sum of the first 6 terms S6
minus the sum of the first 5 terms S5 is the
sixth term a6. That is:
-3.875 = S6 = a1+a2+a3+a4+a5+a6
-3.75 = S5 = a1+a2+a3+a4+a5
-----------------------------------
Subtract those equations term by term
-3.875 - (-3.75) = a6
-3.875 + 3.75 = a6
-0.125 = a6
------------------------------------
So we have found two consecutive terms of the geometric series.
a5 = -0.25
a6 = -0.125
We can find the common ratio by dividing ANY term by the preceding
term, so we can find the common ratio r by dividing the 6th term
by the 5th term:
r = 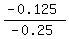 = 0.5
Edwin = 0.5
Edwin
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by ikleyn(53618)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine the common ratio of a geometric series that has these partial sums: S4= -3.5, S5= -3.75, S6= -3.875.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Standard designations mean that S4 is the sum of the first 4 terms of this GP;
S5 is the sum of the first 5 terms of this GP;
S6 is the sum of the first 6 terms of this GP.
Therefore, the 5th terms is S5 - S4 = -3.75 - (-3.5) = -3.75 + 3.5 = -0.25;
the 6th terms is S6 - S5 = -3.875 - (-3.75) = -3.875 + 3.75 = -0.125.
Now we can easily determine the common ratio of this GP.
It is the ratio of the 6th term to the 5th term
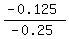 = 0.5. ANSWER = 0.5. ANSWER
Solved.
|
|
|
| |