Question 732891: The first tem of a geometric progression is 7, its last term is 448 and its sum is 889. Find the common ratio
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE LUCKY GUESS APPROACH:
If we call the number of terms  , and the common ratio , and the common ratio  , the last term is , the last term is
 --> -->  --> -->  --> -->

If we are lucky  and and  --> -->  . .
Those numbers would certainly agree with the first term being 7 and the last term being 448.
Would the sum of those 7 terms be 889?
We can figure out the sum using some formula from the book, or we can calculate terms number 2, 3, 4, 5, and 6 and then add all 7 terms.
Either way, we would find out that the sum of the first 7 terms of a geometric progression with ratio 2 and first term 7 is indeed 889.
The approach worked because the problem was design to have nice small numbers as answers for  and and  . .
ANOTHER APPROACH:
The sum of  terms, from terms, from  to to  is is 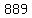
The sum of the first 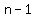 terms, from terms, from  to to 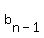 is is
 + ... + + ... +
If we call the common ratio  , ,
 +... + +... + + ... + + ... +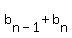
because  , ,  , and so on until , and so on until  , and , and 
 --> -->  --> -->  --> --> 
Since we know 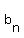 , ,  , and , and  we can calculate we can calculate
 --> -->  --> -->  --> --> 
|
|
|