Question 711986: Determine the number of terms in the following arithmetic sequence: 315, 304, 293, ... , 18.
Found 2 solutions by stanbon, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine the number of terms in the following arithmetic sequence:
315, 304, 293, ... , 18
-----
a = 315
d = 304-315 = -11
----
Solve for "n":
a(n) = a + (n-1)d
----
18 = 315 + (n-1)(-11)
-297 = (n-1)(-11)
n-1 = (-297/-11)
n-1 = 27
n = 28 (# of terms)
=====================
Cheers,
Stan H.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
as you can see, in the following arithmetic sequence, 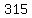 , ,  , , 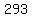 , ... , , ... ,  , the difference between each term is , the difference between each term is  (the fixed amount is called the common difference, (the fixed amount is called the common difference,  ) )
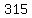

 ...then next term will be ...then next term will be

 ....and so on, up to ....and so on, up to 
To find any term of an arithmetic sequence use formula:
 where where  is the first term of the sequence, is the first term of the sequence,
 is the common difference, is the common difference,  is the number of the term to find is the number of the term to find
in your case is given  , , , and we found that , and we found that 
 ...solve for ...solve for 


 ......plug in given values ......plug in given values




 ......the number of terms ......the number of terms
|
|
|