Question 707572: a tree grows 1.5 meters during the first year of planting. During each subsequent year, the tree grows 9/10 of the previous year's growth. When the growth of the tree since planting is 11.35 meters, its age is?
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! A formula has been developed for this. Terms being like a, ar, ar^2, ar^3,...
for n terms, the sum of those n terms is  .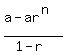
The problem description shows the sum (being 11.35), a=1.5, r=0.9, and the unknown variable is n for the number of years. You might first want to use the formula  , and solve for n. Once done that, THEN substitute the values. Working that way, you should get to
 ; I am dropping the subscript on S just for convenience.
Taking logarithms of both sides whatever base you choose,
Now just substitute the values.
log base ten of [(1.5-11.35(1-.9))/1.5]=-0.6138
log base ten of 0.9=-.045757
n=13.4 years
|
|
|
