Question 696868: hi i'm confused about this question it asks the third term of an arithmitic sequence is 4 and the sum of the first 8 term is 36. write down the first 8 terms of the sequence.
Found 2 solutions by reviewermath, abhishek meena:
Answer by reviewermath(1029)   (Show Source): (Show Source):
You can put this solution on YOUR website! The nth term of an arithmetic sequence is

The third term is 4,therefore
 or or

The sum of the first n terms of an arithmetic sequence is

The sum of the first 8 term is 36,therefore
 or or
 ,divide by 4 ,divide by 4
 , substitute , substitute 


Solve the system


Multiply the first equation by -2


Add the two equations
1 = 3d
d = 1/3, substitute in the first equation and solve for 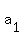

 ,add 1/3 to get the next terms ,add 1/3 to get the next terms
The first 8 terms are:
 , , 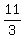 , ,  , , 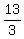 , , 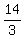 , ,  , , 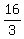 , and , and 
Answer by abhishek meena(6)   (Show Source): (Show Source):
You can put this solution on YOUR website! a(3)=4
s(8)=36
s(n)=(n/2)(2a+(n-1)d)
here n=8
therefore, s(8)=4(2a+7d)=8a+28d=36 - first equation
also a(n)=a+(n-1)d
therefore a(3)=a+2d=4 - second equation
now solve both equation
8(4-2d)+28d=36
32-16d+28d=36
32+12d=36
12d=4
d=1/3
therefore a=4-2d=4-2(1/3)=10/3
now using formula for terms i.e. a(n)=a+(n-1)d
10/3, 11/3, 4, 13/3, 14/3, 5 ,16/3 , 17/3
solved....cheers
my method is easier than mentioned above
|
|
|