SOLUTION: write the geometric series -9/2 + 3/2 - 1/2 + 1/6 - .......... + 1/39366 in summation notation than using the formula for the sum of an geometric series, computer

Algebra ->  Sequences-and-series -> SOLUTION: write the geometric series -9/2 + 3/2 - 1/2 + 1/6 - .......... + 1/39366 in summation notation than using the formula for the sum of an geometric series, computer       Log On


   

Question 696784: write the geometric series -9/2 + 3/2 - 1/2 + 1/6 - .......... + 1/39366 in summation notation




than

using the formula for the sum of an geometric series, computer the sum in the problem above

thanks
Macy Gunderson
Found 2 solutions by Edwin McCravy, josmiceli:
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
-9/2 + 3/2 - 1/2 + 1/6 - .......... + 1/39366
r = 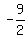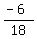3%2F2÷-9%2F2 = 3%2F2×-2%2F9 = %28-6%29%2F18 = -1%2F3

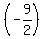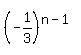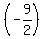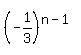
an = a1rn-1 = %28-9%2F2%29×%28-1%2F3%29%5E%28n-1%29 = %28-9%2F2%29×%28-1%2F3%29%5E%28n-1%29

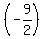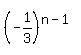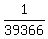%28-9%2F2%29×%28-1%2F3%29%5E%28n-1%29 = 1%2F39366

Multiply both sides by -2%2F9

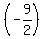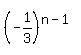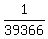
-2%2F9×%28-9%2F2%29×%28-1%2F3%29%5E%28n-1%29 = -2%2F9×1%2F39366

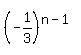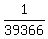
             %28-1%2F3%29%5E%28n-1%29 = -2%2F9×1%2F39366

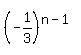             %28-1%2F3%29%5E%28n-1%29 = -2%2F%289%2A39366%29

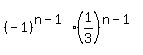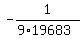
             %28-1%29%5E%28n-1%29%281%2F3%29%5E%28n-1%29 = -1%2F%289%2A19683%29

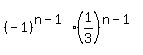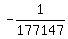             %28-1%29%5E%28n-1%29%281%2F3%29%5E%28n-1%29 = -1%2F177147

n-1 must be an odd number since the right side is negative,
so (-1)n-1 = -1.   Therefore, dividing both sides
by -1,

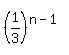             %281%2F3%29%5E%28n-1%29 = 1%2F177147 

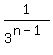             1%2F3%5E%28n-1%29 = 1%2F177147 

taking reciprocals of both sides:

             3n-1 = 177147

Taking the natural log of both sides

           ln(3n-1) = ln(177147)
           (n-1)ln(3) = ln(177147)
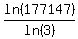                  n-1 = ln%28177147%29%2Fln%283%29
                  n-1 = 11
                    n = 12

So there are 12 terms:

Summation  = sum%28%28-9%2F2%29%28-1%2F3%29%5E%28n-1%29%2C1%2C12%29

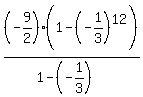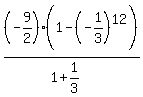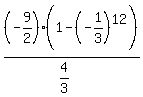Sn = %28a%5B1%5D%281-r%5En%29%29%2F%281-r%29 = %28-9%2F2%29%281-%28-1%2F3%29%5E12%29%2F%281-%28-1%2F3%29%29 = %28-9%2F2%29%281-%28-1%2F3%29%5E12%29%2F%281%2B1%2F3%29 = %28-9%2F2%29%281-%28-1%2F3%29%5E12%29%2F%284%2F3%29


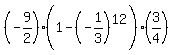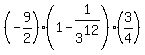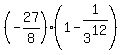= %28-9%2F2%29%281-%28-1%2F3%29%5E12%29%2A%283%2F4%29 = %28-9%2F2%29%281-1%2F3%5E12%29%2A%283%2F4%29 = %28-27%2F8%29%281-1%2F3%5E12%29 = -3.37499365   

The computer program I have is Liberty Basic of which you can download
a free trial version.   Here is the Liberty Basic program I wrote

A1 = -9/2
r = -1/3
for n = 1 to 12
An = A1*r^(n-1)
sum = sum+An
print "A(";n;") = ";An;", sum =";sum
next
 
Here is the output of that program:

A(1) = -4.5, sum =-4.5
A(2) = 1.5, sum =-3
A(3) = -0.5, sum =-3.5
A(4) = 0.16666667, sum =-3.33333333
A(5) = -0.55555556e-1, sum =-3.38888889
A(6) = 0.18518519e-1, sum =-3.37037037
A(7) = -0.61728395e-2, sum =-3.37654321
A(8) = 0.20576132e-2, sum =-3.3744856
A(9) = -0.68587106e-3, sum =-3.37517147
A(10) = 0.22862369e-3, sum =-3.37494284
A(11) = -0.76207895e-4, sum =-3.37501905
A(12) = 0.25402632e-4, sum =-3.37499365
  
Edwin

Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
Let the numbering of the terms be
1,2,3,4, . . . etc.
The changing sign part goes
term #1 is (-)
term #2 is (+)
term #3 is (-)
etc.
That part of the general formula is
+%28-1%29%5En+ where +n+ is the number of the term
------------
It looks like I might be able to have a +1%2F2+ in each
term, so i've got so far:
+%281%2F2%29%2A%28-1%29%5En+
But, obviously, that's not all of it.
What if I put in a factor of +3%5E%28+3-n%29+ ? Now I have
+%281%2F2%29%2A%28+3%5E%283-n%29+%29%2A%28-1%29%5En+
I'll test it out
+n+=+1+
+%281%2F2%29%2A%28+3%5E%283-1%29%29%2A%28-1%291%5E1+=+%281%2F2%29%2A9%2A%28-1%29+
+-9%2F2+
---------
+n+=+2+
+%281%2F2%29%2A%28+3%5E%283-2%29%29%2A%28-1%291%5E2+=+%281%2F2%29%2A3%2A1+
+3%2F2+
---------
+n+=+3+
+%281%2F2%29%2A%28+3%5E%283-3%29%29%2A%28-1%291%5E3+=+%281%2F2%29%2A3%5E0%2A%28-1%29+
+-1%2F2+
----------
+n+=+4+
+%281%2F2%29%2A%28+3%5E%283-4%29%29%2A%28-1%291%5E4+=+%281%2F2%29%2A3%5E%28-1%29%2A1+
+1%2F6+
This works
So the formula is
+%281%2F2%29%2A%28+3%5E%283-n%29+%29%2A%28-1%29%5En+
I'm not sure about the summation notation. Are they
looking for the sum of all the terms?
Us the sigma ( summation ) symbol in front
of what I just gave you.