SOLUTION: Hello I had a question regarding arithmetic sequences. Here we have 1+3+5+...+915. How would I find the sum using a formula? Thank You all for your time to help and teach.

Algebra ->  Sequences-and-series -> SOLUTION: Hello I had a question regarding arithmetic sequences. Here we have 1+3+5+...+915. How would I find the sum using a formula? Thank You all for your time to help and teach.       Log On


   

Question 694434: Hello I had a question regarding arithmetic sequences.
Here we have 1+3+5+...+915.
How would I find the sum using a formula?
Thank You all for your time to help and teach.
Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

Hello I had a question regarding arithmetic sequences.
Here we have 1+3+5+...+915.
How would I find the sum using a formula?
Thank You all for your time to help and teach.

This problem can be solved by using the number of numbers formula: n+=+%28a%5Bn%5D+-+a%5B1%5D%29%2F2+%2B+1, first, to determine the number of numbers, or "n," with a%5B1%5D being the first term, and = 1, and a%5Bn%5D being the last term, and = 915.

n+=+%28915+-+1%29%2F2+%2B+1 ----- n+=+%28914%2F2%29+%2B+1 ----- n+=+457+%2B+1 ----- n+=+458


The formula for sum of an arithmetic sequence, or A.P. is: S%5Bn%5D+=+%28n%2F2%29%282a%5B1%5D+%2B+%28n+-+1%29d%29, with S%5Bn%5D+=+S%5B458%5D, 1st term, or a%5B1%5D = 1; n, or amount of terms to be summed = 458, and d, or common difference = 2

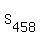Therefore, S%5Bn%5D+=+%28n%2F2%29%282a%5B1%5D+%2B+%28n+-+1%29d%29 becomes: S%5B458%5D+=+%28458%2F2%29%282%281%29+%2B+%28458+-+1%292%29

S%5B458%5D+=+229%282+%2B+%28457%292%29

S%5B458%5D+=+229%282+%2B+914%29

S%5B458%5D+=+229%28916%29

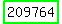
S%5B458%5D, or sum of the 458 terms in the series = highlight_green%28209764%29

You can do the check!!

Send comments and “thank-yous” to “D” at MathMadEzy@aol.com