Question 691008: three numbers whose sum is 24 are in A.P. if the first is decreased by 1 , the second is decreased by 2 and third is not changed, then the resulting numbers are in G.P. find them
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Middle numbers can be very useful in arithmetic progressions, even if the wording does not refer to an A.P., as in "three consecutive odd numbers".
You may have been told that if three numbers are in arithmetic progression, the middle one is the average of the other two (and the average of all three).
So, the middle number is the sum, divided by  : :  . .
 = common difference of the A.P. = common difference of the A.P.
The three numbers in the A.P., in order, are:
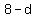 , ,  , and , and 
If the first is decreased by 1 , the second is decreased by 2 and third is not changed, then the resulting numbers are:
 , ,  , and , and 
If those numbers are in a geometric progression, the common ratio,
calculated from the first two, or from the last two is the same, so

From that equation, I can solve for  . .
 --> -->  (equating the cross-products or multiplying both sides times (equating the cross-products or multiplying both sides times 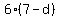 , whichever you prefer as an explanation) , whichever you prefer as an explanation)
 --> -->  --> -->  --> --> 
Rearranging, and multiplying both sides times  , I get the equation in a form I like better: , I get the equation in a form I like better:
 --> -->  --> -->  --> --> 
Now, I can solve that quadratic equation by factoring:
 --> -->  --> -->  or or  , the 3 numbers are 3, 8, and 13: , the 3 numbers are 3, 8, and 13:
 --> -->  , ,  , and , and  --> --> 
With  , the 3 numbers are 14, 8, and 2: , the 3 numbers are 14, 8, and 2:
 --> -->  --> -->  , ,  , and , and  --> -->  --> --> 
|
|
|