SOLUTION: the sum of first 10 terms of an AP is -80 and sum of next 10 terms is -280.find the A.P n

The sum formula for the first n terms of an AP is:

Sn = [2a1 + (n-1)·d]

n = 10, Sn = -80

-80 = [2a1 + (10-1)·d]

-80 = 5·[2a1 + 9d]

Dividing through by 5,

-16 = 2a1 + 9d 

Therefore the sum of the first 20 terms is the sum
of the first 10 terms which is -80 PLUS the sum of
the next 10 terms, which is given to be -280.  That 
makes the sum of the first 20 terms -80-280 = -360.

So now we have

Sn = [2a1 + (n-1)·d], this time with

n = 20, Sn = -360

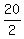-360 = [2a1 + (20-1)·d]

-360 = 10·[2a1 + 19d]

Dividing through by 10,

-36 = 2a1 + 19d 

So we have this system of equations:

-16 = 2a1 +  9d
-36 = 2a1 + 19d

Subtracting those two equations term by term,

 20 = -10d

 -2 = d

Substituting in

-16 = 2a1 + 9d
-16 = 2a1 + 9(-2)
-16 = 2a1 - 18
  2 = 2a1
  1 = a1

The AP then is:

1, -1, -3, -5, -7, -9, -11, -13, -15, -17, -19,
-21, -23, -25, -27, -29, -31, -33, -35, -37, -39, -41,
-43, -45, -47, -49, -51, -53, -55, -57, -59, -61, -63,
-65, -67, -69, -71, -73, -75, -77, -79, -81, -83, -85,
-87, -89, -91, -93, -95, -97, -99, -101, -103, -105, -107,
-109, -111, -113, -115, -117, -119, -121, -123, -125, -127, -129,
-131, -133, -135, -137, -139, -141, -143, -145, -147, -149, -151,
-153, -155, -157, -159, -161, -163, -165, -167, -169, -171, -173,
-175, -177, -179, -181, -183, -185, -187, -189, -191, -193, -195,
-197, ... 

Edwin