Question 662463: Question: The arithmetic series 5 + 9 + 13 + ... + tn has a sum of 945. How many terms does the series have?
I was just having an issue trying to figure out what formula to use. Any help would be greatly appreciated.
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum s of an arithmetic series with first term  , ,  terms, and common difference terms, and common difference  is: is:

Applying this to the given series:







 ...factor...replace ...factor...replace  with with 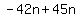
 ....group ....group



The positive root  gives the gives the  of of  . .
so, your sequence is:
 , ,  , ,  , , , , , , , , , , , , , , , , , ,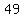 , , , ,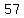 , ,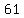 , , , ,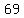 , , , , , ,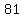 , ,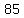
the sum is:


Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
5 + 9 + 13 + ... + tn = 945
We need the sum formula:
Sn =  [2t1 + (n-1)·d]
To find d, the common difference, we subtract the first term,
t1 = 5 from the second term t2 = 9, and
get 9-5 = 4, and as a check we also subtract the second term,
t2 = 9 from the third term t3 = 12, and
get 13-9 = 4, so the common difference d is 4. So we substitute
d = 4, Sn = 945, t1 = 5 and solve for n:
Sn = [2t1 + (n-1)·d]
To find d, the common difference, we subtract the first term,
t1 = 5 from the second term t2 = 9, and
get 9-5 = 4, and as a check we also subtract the second term,
t2 = 9 from the third term t3 = 12, and
get 13-9 = 4, so the common difference d is 4. So we substitute
d = 4, Sn = 945, t1 = 5 and solve for n:
Sn =  [2t1 + (n-1)·d]
945 = [2t1 + (n-1)·d]
945 =  [2·5 + (n-1)·4]
Multiply both sides by 2 to clear the fraction on the right:
1890 = n[10 + (n-1)·4]
1890 = n[10 + 4(n-1)]
1890 = n[10 + 4n - 4]
1890 = n[4n + 6]
1890 = 4n² + 6n
Divide through by 2
945 = 2n² + 3n
Get 0 on the left
0 = 2n² + 3n - 945
The right side factors as
0 = (n - 21)(2n + 45)
Use the zero-factor property:
n - 21 = 0; 2n + 45 = 0
n = 21; 2n = -45
n = [2·5 + (n-1)·4]
Multiply both sides by 2 to clear the fraction on the right:
1890 = n[10 + (n-1)·4]
1890 = n[10 + 4(n-1)]
1890 = n[10 + 4n - 4]
1890 = n[4n + 6]
1890 = 4n² + 6n
Divide through by 2
945 = 2n² + 3n
Get 0 on the left
0 = 2n² + 3n - 945
The right side factors as
0 = (n - 21)(2n + 45)
Use the zero-factor property:
n - 21 = 0; 2n + 45 = 0
n = 21; 2n = -45
n = 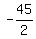 Ignore the negative answer.
It has 21 terms.
5 + 9 + 13 + 17 + 21 + 25 + 29 + 33 + 37 + 41 + 45 + 49 + 53 + 57 + 61 + 65 + 69 + 73 + 77 + 81 + 85
Edwin
Ignore the negative answer.
It has 21 terms.
5 + 9 + 13 + 17 + 21 + 25 + 29 + 33 + 37 + 41 + 45 + 49 + 53 + 57 + 61 + 65 + 69 + 73 + 77 + 81 + 85
Edwin
|
|
|