Question 6528: How do I find the standard deviation to the nearest tenth of the following set of data? {47, 61, 93, 22, 82, 22, 37}
Answer by Mike(39)   (Show Source): (Show Source):
You can put this solution on YOUR website! Firstly, there are two different types of standard deviation - population standard deviation and sample standard deviation. I assume you are trying to find the population standard deviation, because that is the most common.
In order to find the population standard deviation without the use of a calculator, you need to first establish the mean(µ) of your set of data. The µ of your set of data is: 52. You must now establish how much each one of your marks(M) deviates from the µ (i.e. 47 - 52, 61 - 52, etc. etc.). You then square that deviation and multiply it by the frequency (f) of that mark(M) (the entire formula for this procedure is f(M-µ)^2). Let me show you what I mean:
1) 47 - 52 = -5
2) -5^2 = 25
3) f is equal to 1 because it only appears once in your set of data.
Therefore, in this case, f(M-µ)^2) = 1(47-52)^2 = 25
For the others:
1(61-52)^2 = 81
1(93-52)^2 = 1681
2(22-52)^2 = 1800
1(82-52)^2 = 900
1(37-52)^2 = 225
You now add all of these answers up and divide them by the number of data points you have (7 in this case: 47, 61, 93, 22, 82, 22, 37)
25+81+1681+1800+900+225 = 4712/7 = 673.14. This is known as the Variance.
In order to obtain the population standard deviation, all you now need to do is take the square root of the variance.
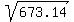 = 25.94 = 25.94
This entire procedure is a whole lot easier to do if you have a graphing calculator like the Ti-83, but being dependent on your calculator is never a good thing.
If you have any more questions let me know.
Regards,
-Mike
|
|
|