Question 597021: Hi. Can someone please teach me how to solve this question? It's quite easy but I want to know how. It would mean a lot. Thanks!
How many integers between 197 and 303 are divisible by 4 or 10?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A GENERAL APPROACH TO THIS TYPE OF PROBLEM:
Numbers divisible by 4 (also called multiples of 4) can be written as 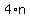 , where , where  in meant to be an integer. in meant to be an integer.
The first one is  . .
Multiple number 49 is  . .
Counting all between multiple number 50,  and and
multiple number 75,  , there are , there are  . .
Numbers divisible by 10 (also called multiples of 10) can be written as 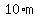 , where , where  in meant to be an integer. in meant to be an integer.
The first one is  . .
Multiple number 19 is  . .
Counting all between multiple number 20,  and and
multiple number 30,  , there are , there are  . .
Numbers that are divisible by 4 and by 10, are also divisible by their least common multiple, 20, and we should be careful not to count them twice.
Since there are only a few between 197 and 300, I'll just count them. It's just 200, 220, 240, 260, 280, and 300, just 6 of them.
The numbers between 197 and 303 that are divisible by 4 or by 10 are the 26 that are divisible by 4, plus the 11 divisible by 10, minus the 6 that are divisible by both, so it is

ALTERNATE APPROACH (for when there are not too many numbers to count):
In this case, we could also had carefully listed and counted the numbers.
200, 204, 208, 210, 212,
216, 220, 224, 228, 230,
232, 236, 240, 244, 248,
250, 252, 256, 260, 264,
268, 270, 272, 276, 280,
284, 288, 290, 292, 296, and
300.
|
|
|