Question 568043: please explain how to find only thee sum of the odd numbers in sigma notation n=1-35
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You could say that odd numbers can be written as  . .
All odd numbers can be written that way for some natural number  , and the expression , and the expression  gives you an odd number for every natural number gives you an odd number for every natural number  . .
 , ,  , ... , ... 
You are trying to find the sum of the first 18 odd numbers:
S=1+3+5+ ... +31+33+35
There are many ways to go about it.
BLAZING YOUR OWN TRAIL (or rediscovering gunpowder):
2S=S+S=(1+3+5+ ... +31+33+35)+(1+3+5+ ... +31+33+35)=1+3+5+ ... +31+33+35+1+3+5+ ... +31+33+35.
Because of commutative and associative properties, we can re-arrange that sum, pairing the first number with the last, second with second last, and so on, to get:
2S=(1+35)+(3+33)+(5+31)+ ... +(31+5)+(33+3)+(35+1)=36+36+36+ ... +36+36+36=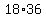
2S=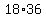 --> S= --> S=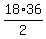 =324 =324 
INVOKING ARITHMETIC SEQUENCES (if that's what you are studying)
The sum that you want is 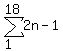
That is the sum of an arithmetic sequence (or arithmetic progression). You may write the terms explicit formula as  , with first term , with first term  and common difference and common difference  . .
(That is equivalent to  ). ).
Naming conventions may vary, and you may use 
You may have been given the formula:
 or or 
You would calculate
 or or
knowing  from the start, you may rather calculate from the start, you may rather calculate

Or maybe your naming conventions and formulas are a bit different.
Anyway, you'll get the answer 
INVOKING KNOWN SUMS
You may have been told that the sum of the fist n natural numbers is
1+2+3+ ...+(n-1)+n=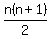
Then, the sum of all integers from 1 to 35 is  and can be written as the sum of the odd numbers from 1 to 25 plus the sum of the first 17 even numbers from 2 to 34: and can be written as the sum of the odd numbers from 1 to 25 plus the sum of the first 17 even numbers from 2 to 34:

The sum of the first 17 even numbers is twice the sum of the first 17 natural numbers:
(2+
So  --> --> 
Anyway, you'll get the answer 
|
|
|