Question 529087: Consider the sequence x-3, x+1, 2x+8. One value for x is 5, making the sequence geometric.
find the other value of x for which the sequence is geometric
For this value of x find the common ratio and the sum of the infinite sequence
Found 2 solutions by KMST, Edwin McCravy:
Answer by KMST(5328)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor's solution is incorrect.
x-3, x+1, 2x+8
Let r = the common ratio
Then we have the system of two equations in two unknowns:
r(x-3) = x+1
r(x+1) = 2x+8
Solving each for r:
r = 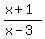 r =
r =  Setting the right sides equal to each other, since both
equal to r:
Setting the right sides equal to each other, since both
equal to r:
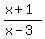 = =  Cross-multiplying:
(x+1)(x+1) = (x-3)(2x+8)
x² + 2x + 1 = 2x² + 2x - 24
0 = x² - 25
0 = (x - 5)(x + 5)
x - 5 = 0 x + 5 = 0
x = 5 x = -5
As they told us, x = 5 is one of the values and it
makes the sequence
x-3, x+1, 2x+8 become
5-3, 5+1, 2(5)+8
2, 6, 18
and the common ratio is
Cross-multiplying:
(x+1)(x+1) = (x-3)(2x+8)
x² + 2x + 1 = 2x² + 2x - 24
0 = x² - 25
0 = (x - 5)(x + 5)
x - 5 = 0 x + 5 = 0
x = 5 x = -5
As they told us, x = 5 is one of the values and it
makes the sequence
x-3, x+1, 2x+8 become
5-3, 5+1, 2(5)+8
2, 6, 18
and the common ratio is 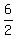 = =  = 3.
The other value of x is -5. It makes the sequence
x-3, x+1, 2x+8 become:
-5-3, -5+1, 2(-5)+8
-8, -6, -2
and the ratio is = 3.
The other value of x is -5. It makes the sequence
x-3, x+1, 2x+8 become:
-5-3, -5+1, 2(-5)+8
-8, -6, -2
and the ratio is  = =  = =  Since the common ratio is less than 1, we can sum the series
to infinity with the equation:
Since the common ratio is less than 1, we can sum the series
to infinity with the equation:
 = = 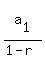 where
where  is the first term -8, and r = is the first term -8, and r =  Substituting:
Substituting:
 = = 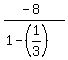 = = 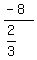 = = 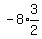 = -12.
Edwin = -12.
Edwin
|
|
|